Data Handling

Data handling

Definition:

Data:

• facts and statistics collected together for reference or analysis.
• the quantities, characters, or symbols on which operations are performed by a computer, which may be stored and transmitted in the form of electrical signals and recorded on magnetic, optical, or mechanical recording media.
• things known or assumed as facts, making the basis of reasoning or calculation.

Handling:

• a touching, grasping, or using with the hands.
• the manner of treating or dealing with something; management;treatment.
• the manual or mechanical method or process by which something is moved, carried, transported, etc.
• of or relating to the process of moving, transporting, delivering,working with, etc.:

Data handling is the process of ensuring that research data is stored, archived or disposed off in a safe and secure manner during and after the conclusion of a research project. This includes the development of policies and procedures to manage data handled electronically as well as through non-electronic means .

Introduction: 

you have probably seen diagrams and charts in magazines and newspapers. such diagrams are used to tell you, in a summarized form, about the way in wich certain quantities or numbers of objects vary

Data is a collection of facts, such as numbers, words, measurements observations or even just descriptions of things. when collecting data in a survey the following precautions must be taken to ensure that all results are unbiased 

• the sample of the population from whom the data is collected must be randomly chosen 
• the members of the sample must be proportional to the members of the population 
• the sample must not be too small as it would then be difficult to draw conclusions

collecting data

remember to check out my youtube channel  https://www.youtube.com/channel/UCC9x0RneGT_qSah_DRlzGHg

geometry

definition:

the branch of mathematics concerned with the properties and relations of points, lines, surfaces, solids, and higher dimensional analogues.

Geometry (from the Ancient Greek: γεωμετρία; geo- "earth", -metron "measurement") is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. A mathematician who works in the field of geometry is called a geometer.

Points

Main article: Point (geometry)

Points are considered fundamental objects in Euclidean geometry. They have been defined in a variety of ways, including Euclid's definition as 'that which has no part'^[31] and through the use of algebra or nested sets.^[32] In many areas of geometry, such as analytic geometry, differential geometry, and topology, all objects are considered to be built up from points. However, there has been some study of geometry without reference to points.^[33]

Lines

Main article: Line (geometry)

Euclid described a line as "breadthless length" which "lies equally with respect to the points on itself".^[31] In modern mathematics, given the multitude of geometries, the concept of a line is closely tied to the way the geometry is described. For instance, in analytic geometry, a line in the plane is often defined as the set of points whose coordinates satisfy a given linear equation,^[34] but in a more abstract setting, such as incidence geometry, a line may be an independent object, distinct from the set of points which lie on it.^[35] In differential geometry, a geodesic is a generalization of the notion of a line to curved spaces.^[36]

Planes

Main article: Plane (geometry)

A plane is a flat, two-dimensional surface that extends infinitely far.^[31] Planes are used in every area of geometry. For instance, planes can be studied as a topological surface without reference to distances or angles;^[37] it can be studied as an affine space, where collinearity and ratios can be studied but not distances;^[38] it can be studied as the complex plane using techniques of complex analysis;^[39] and so on.

Angles

Main article: Angle

Euclid defines a plane angle as the inclination to each other, in a plane, of two lines which meet each other, and do not lie straight with respect to each other.^[31] In modern terms, an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle.^[40]

Acute (a), obtuse (b), and straight (c) angles. The acute and obtuse angles are also known as oblique angles.

In Euclidean geometry, angles are used to study polygons and triangles, as well as forming an object of study in their own right.^[31] The study of the angles of a triangle or of angles in a unit circle forms the basis of trigonometry.^[41]

In differential geometry and calculus, the angles between plane curves or space curves or surfaces can be calculated using the derivative.^[42][43]

Curves

Main article: Curve (geometry)

A curve is a 1-dimensional object that may be straight (like a line) or not; curves in 2-dimensional space are called plane curves and those in 3-dimensional space are called space curves.^[44]

In topology, a curve is defined by a function from an interval of the real numbers to another space.^[37] In differential geometry, the same definition is used, but the defining function is required to be differentiable ^[45] Algebraic geometry studies algebraic curves, which are defined as algebraic varieties of dimension one.^[46]

Surfaces

Main article: Surface (mathematics)

A sphere is a surface that can be defined parametrically (by x = r sin θ cos φ, y = r sin θ sin φ, z = r cos θ) or implicitly (by x² + y² + z² − r² = 0.)

A surface is a two-dimensional object, such as a sphere or paraboloid.^[47] In differential geometry^[45] and topology,^[37] surfaces are described by two-dimensional 'patches' (or neighborhoods) that are assembled by diffeomorphisms or homeomorphisms, respectively. In algebraic geometry, surfaces are described by polynomial equations.^[46]

Manifolds

Main article: Manifold

A manifold is a generalization of the concepts of curve and surface. In topology, a manifold is a topological space where every point has a neighborhood that is homeomorphic to Euclidean space.^[37] In differential geometry, a differentiable manifold is a space where each neighborhood is diffeomorphic to Euclidean space.^[45]

Manifolds are used extensively in physics, including in general relativity and string theory

Sources

https://en.wikipedia.org/wiki/Geometry

If you like playing with objects, or like drawing, then geometry is for you!

Geometry can be divided into: 

	Plane Geometry is about flat shapes like lines, circles and triangles ... shapes that can be drawn on a piece of paper
	Solid Geometry is about three dimensional objects like cubes, prisms, cylinders and spheres.

Hint: Try drawing some of the shapes and angles as you learn ... it helps.

Point, Line, Plane and Solid

A Point has no dimensions, only position
A Line is one-dimensional
A Plane is two dimensional (2D)
A Solid is three-dimensional (3D)

Why?

Why do we do Geometry? To discover patterns, find areas, volumes, lengths and angles, and better understand the world around us.

Plane Geometry

Plane Geometry is all about shapes on a flat surface (like on an endless piece of paper).

• 2D Shapes
•  Activity: Sorting Shapes
• Triangles
• Right Angled Triangles
• Interactive Triangles

• Quadrilaterals (Rhombus, Parallelogram, etc)
• Rectangle, Rhombus, Square, Parallelogram, Trapezoid and Kite
• Interactive Quadrilaterals
• Shapes Freeplay

• Perimeter

• Area
• Area of Plane Shapes
• Area Calculation Tool
• Area of Polygon by Drawing
• Activity: Garden Area

• General Drawing Tool

Polygons

A Polygon is a 2-dimensional shape made of straight lines. Triangles and Rectangles are polygons.

Here are some more:

Pentagon

Pentagram

Hexagon

• Properties of Regular Polygons
• Diagonals of Polygons
• Interactive Polygons

The Circle

• Circle
• Pi
• Circle Sector and Segment
• Circle Area by Sectors
• Annulus
• Activity: Dropping a Coin onto a Grid

Circle Theorems (Advanced Topic)

Symbols

There are many special symbols used in Geometry. Here is a short reference for you:

Geometric Symbols

Congruent and Similar

• Congruent Shapes
• Similar Shapes

Angles

Types of Angles

Acute Angles

Right Angles

Obtuse Angles

Straight Angle

Reflex Angles

Full Rotation

Degrees (Angle) Radians Congruent Angles Parallel Lines and Pairs of Angles Transversal A Triangle Has 180° Supplementary Angles Complementary Angles

Angles Around a Point Angles on a Straight Line Interior Angles Exterior Angles Interior Angles of Polygons Exterior Angles of Polygons

Using Drafting Tools Geometric Constructions Using the Protractor Using the Drafting Triangle and Ruler Using a Ruler and Compass

Transformations and Symmetry

Transformations:

• Rotation
• Reflection
• Translation
• Resizing

Symmetry:

• Reflection Symmetry
• Rotational Symmetry
• Point Symmetry
• Lines of Symmetry of Plane Shapes

• Symmetry Artist

• Activity: Symmetry of Shapes
• Activity: Make a Mandala
• Activity: Coloring (The Four Color Theorem)

• Tessellations
• Tessellation Artist

Coordinates

• Cartesian Coordinates
• Interactive Cartesian Coordinates
• Hit the Coordinate Game

More Advanced Topics in Plane Geometry

Pythagoras

• Pythagoras' Theorem
• Pythagorean Triples

Conic Sections

• Set of all points
• Conic Sections
• Ellipse
• Parabola
• Hyperbola

Trigonometry

Trigonometry is a special subject of its own, so you might like to visit:

• Introduction to Trigonometry
• Trigonometry Index

Solid Geometry

Solid Geometry is the geometry of three-dimensional space - the kind of space we live in ...

... let us start with some of the simplest shapes:

Common 3D Shapes

Polyhedra and Non-Polyhedra

There are two main types of solids, "Polyhedra", and "Non-Polyhedra":

Polyhedra : (they must have flat faces)	Cubes and Cuboids (Volume of a Cuboid)      Platonic Solids    Prisms    Pyramids
Non-Polyhedra: (if any surface is not flat)	Sphere Torus Cylinder Cone

• Polyhedron Models
• Vertices, Faces, and Edges
• Cone vs Sphere vs Cylinder
• Euler's Theorem

Sources

https://www.mathsisfun.com/geometry/

more coming soon

perpendicular lines:

In elementary geometry, the property of being perpendicular(perpendicularity) is the relationship between two lines which meet at a right angle (90 degrees). The property extends to other related geometric objects. A line is said to be perpendicular to another line if the two lines intersect at a right angle.

Perpendicular

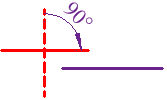
It just means at right angles (90°) to.

The red line is perpendicular to the blue line in both these cases:

(The little box drawn in the corner, means "at right angles", so we didn't really need to also show that it was 90°, but we just wanted to!)

Parallel

Lines are parallel if they are always the same distance apart (called "equidistant"), and will never meet. (They also point in the same direction). Just remember:

Always the same distance apart and never touching.

example 2

The red line and blue line are parallel in both these examples:

Example 1

Perpendicular to Parallel

Question: What is the difference between perpendicular and parallel? 
Answer: 90 degrees (a right angle)
That's right, when we rotate a perpendicular line by 90° it becomes parallel (but not if it touches!)

Perpendicular ...	Rotate One Line 90°	... Parallel !

Likewise, parallel lines become perpendicular when one line is rotated 90°.

Parallel Curves

Curves can also be parallel when they are always the same distance apart (called "equidistant"), and never meet. Just like railroad tracks.
The red curve is parallel to the blue curve in both these cases:

Parallel Surfaces

Surfaces can also be parallel, so long as the rule still holds: always the same distance apart and never touching.

Lines and Planes

Advanced Topic: You can also learn about Parallel and Perpendicular Lines and Planes

 https://www.mathsisfun.com/perpendicular-parallel.html

Perpendicular Lines

Let's graph these lines:

* I'm using y = mx + b stuff to graph them!
 

These lines are perpendicular. (They form a angle.) So, what's going on with the slopes? Notice that they are inverses but the signs are different

A typical math book would say:

But this is easier:

You flip it over and change the sign -- That's how you get the slopes of perpendicular lines.

* If you want to be a super geek, you can rap it!

Check it out:

Take the 2 ... Write it as a fraction: 

Flip it over:   ... and change the sign: 

Let's do a problem:

Let's find the equation of the line that passes through the point
( 1 , 3 ) and is perpendicular to the line		.

What do we need?

a point

a slope

STEP 1:  Find the slope

It's perpendicular to

...

So, we'll get this guy's slope ...  flip it and change the sign!  Easy!

STEP 2: Use the point-slope formula with ( 1 , 3)              and m = 

Graph		and		and see if they
really look perpendicular.

---

TRY IT:

Find the equation of the line that passes through the point ( -2 , 2 ) and is perpendicular to the line

http://www.coolmath.com/algebra/08-lines/14-perpendicular-lines-03

Perpendicular lines (Coordinate Geometry) When two lines are perpendicular, the slope of one is the negative reciprocal of the other. If the slope of one line is m, the slope of the other is  Try this Drag points C or D. Note the slopes when the lines are at right angles to each other. When two lines are perpendicular to each other (at right angles or 90°), their slopes have a particular relationship to each other. If the slope of one line is m then the slope of the other line is the negative reciprocal of m, or So for example in the figure above, the line AB has a slope of 0.5, meaning it goes up by a half for every one across. The line CD if it is perpendicular to AB has a slope of -1/0.5 or -2. Adjust points C or D to make CD perpendicular to AB and verify this result. Fig 1. Lines are still perpendicular Remember that the equation works both ways, so it doesn't matter which line you start with. In the figure above the slope of CD is -2. So the slope of AB when perpendicular is Note too that the lines to do not have to intersect to be perpendicular. In Fig 1, the two lines are perpendicular to each other even though they do not touch. The slope relationship still holds. 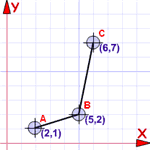Example 1.   Are two lines perpendicular? Fig 1. Are these lines perpendicular? In Fig 1, the line AB and a line segment CD appear to be at right angles to each other. Determine if this is true. To do this, we find the slope of each line and then check to see if one slope is the negative reciprocal of the other. If the lines are perpendicular, each will be the negative reciprocal of the other. It doesn't matter which line we start with, so we will pick AB:  Calculator So, the slope of CD is -2.22, and the negative reciprocal of the slope of AB is -2.79. These are not the same, so the lines are not perpendicular, even though they look it. If you look carefully at the diagram, you can see that the point C is a little too far to the left for the lines to be perpendicular. Example 2. Define a line through a point perpendicular to a line In Fig 1, find a line through the point E that is perpendicular to CD. The point E is on the y-axis and so is the y-intercept of the desired line. Once we know the slope of the line, we can express it using its equation in slope-intercept form y=mx+b, where m is the slope and b is the y-intercept. First find the slope of the line CD: The line we seek will have a slope which is the negative reciprocal of this: The intercept is 10, the point where the line will cross the y-axis. Substituting these values into the equation, the line we need is described by the equation y = 0.45x + 10 This is one of the ways a line can be defined and so we have solved the problem. If we wanted to plot the line, we would find another point on the line using the equation and then draw the line through that point and the intercept. For more on this see Equation of a Line (slope - intercept form) http://www.mathopenref.com/coordperpendicular.html