definition:
the branch of mathematics concerned with the properties and relations of points, lines, surfaces, solids, and higher dimensional analogues.
Geometry (from the Ancient Greek: γεωμετρία; geo- "earth", -metron "measurement") is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. A mathematician who works in the field of geometry is called a geometer.
Points
Main article: Point (geometry)
Points are considered fundamental objects in Euclidean geometry. They have been defined in a variety of ways, including Euclid's definition as 'that which has no part'[31] and through the use of algebra or nested sets.[32] In many areas of geometry, such as analytic geometry, differential geometry, and topology, all objects are considered to be built up from points. However, there has been some study of geometry without reference to points.[33]
Lines
Main article: Line (geometry)
Euclid described a line as "breadthless length" which "lies equally with respect to the points on itself".[31] In modern mathematics, given the multitude of geometries, the concept of a line is closely tied to the way the geometry is described. For instance, in analytic geometry, a line in the plane is often defined as the set of points whose coordinates satisfy a given linear equation,[34] but in a more abstract setting, such as incidence geometry, a line may be an independent object, distinct from the set of points which lie on it.[35] In differential geometry, a geodesic is a generalization of the notion of a line to curved spaces.[36]
Planes
Main article: Plane (geometry)
A plane is a flat, two-dimensional surface that extends infinitely far.[31] Planes are used in every area of geometry. For instance, planes can be studied as a topological surface without reference to distances or angles;[37] it can be studied as an affine space, where collinearity and ratios can be studied but not distances;[38] it can be studied as the complex plane using techniques of complex analysis;[39] and so on.
Angles
Main article: Angle
Euclid defines a plane angle as the inclination to each other, in a plane, of two lines which meet each other, and do not lie straight with respect to each other.[31] In modern terms, an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle.[40]
In Euclidean geometry, angles are used to study polygons and triangles, as well as forming an object of study in their own right.[31] The study of the angles of a triangle or of angles in a unit circle forms the basis of trigonometry.[41]
In differential geometry and calculus, the angles between plane curves or space curves or surfaces can be calculated using the derivative.[42][43]
Curves
Main article: Curve (geometry)
A curve is a 1-dimensional object that may be straight (like a line) or not; curves in 2-dimensional space are called plane curves and those in 3-dimensional space are called space curves.[44]
In topology, a curve is defined by a function from an interval of the real numbers to another space.[37] In differential geometry, the same definition is used, but the defining function is required to be differentiable [45] Algebraic geometry studies algebraic curves, which are defined as algebraic varieties of dimension one.[46]
Surfaces
Main article: Surface (mathematics)
A surface is a two-dimensional object, such as a sphere or paraboloid.[47] In differential geometry[45] and topology,[37] surfaces are described by two-dimensional 'patches' (or neighborhoods) that are assembled by diffeomorphisms or homeomorphisms, respectively. In algebraic geometry, surfaces are described by polynomial equations.[46]
Manifolds
Main article: Manifold
A manifold is a generalization of the concepts of curve and surface. In topology, a manifold is a topological space where every point has a neighborhood that is homeomorphic to Euclidean space.[37] In differential geometry, a differentiable manifold is a space where each neighborhood is diffeomorphic to Euclidean space.[45]
Manifolds are used extensively in physics, including in general relativity and string theory
Sources
If you like playing with objects, or like drawing, then geometry is for you!
Geometry can be divided into:
 | Plane Geometry is about flat shapes like lines, circles and triangles ... shapes that can be drawn on a piece of paper |
 | Solid Geometry is about three dimensional objects like cubes, prisms, cylinders and spheres. |
| Hint: Try drawing some of the shapes and angles as you learn ... it helps. |
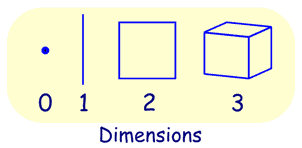
Point, Line, Plane and Solid
A Point has no dimensions, only position
A Line is one-dimensional
A Plane is two dimensional (2D)
A Solid is three-dimensional (3D)
A Line is one-dimensional
A Plane is two dimensional (2D)
A Solid is three-dimensional (3D)
Why?
Why do we do Geometry? To discover patterns, find areas, volumes, lengths and angles, and better understand the world around us.
Plane Geometry
Plane Geometry is all about shapes on a flat surface (like on an endless piece of paper).
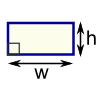
- Quadrilaterals (Rhombus, Parallelogram, etc)
- Rectangle, Rhombus, Square, Parallelogram, Trapezoid and Kite
- Interactive Quadrilaterals
- Shapes Freeplay
Polygons
A Polygon is a 2-dimensional shape made of straight lines. Triangles and Rectangles are polygons.
Here are some more:
The Circle
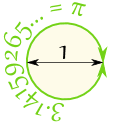
- Circle
- Pi
- Circle Sector and Segment
- Circle Area by Sectors
- Annulus
 Activity: Dropping a Coin onto a Grid
Activity: Dropping a Coin onto a Grid
Circle Theorems (Advanced Topic)
Symbols
There are many special symbols used in Geometry. Here is a short reference for you:
Congruent and Similar
Angles
|
|
|
 | Using Drafting Tools |  |
Transformations and Symmetry

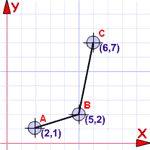
Coordinates
More Advanced Topics in Plane Geometry
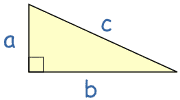
Pythagoras
Conic Sections

Trigonometry
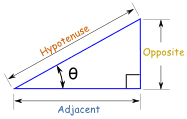
Trigonometry is a special subject of its own, so you might like to visit:
Solid Geometry
Solid Geometry is the geometry of three-dimensional space - the kind of space we live in ...
... let us start with some of the simplest shapes:
Polyhedra and Non-Polyhedra
There are two main types of solids, "Polyhedra", and "Non-Polyhedra":
| Polyhedra : (they must have flat faces) |
| ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Non-Polyhedra: (if any surface is not flat) |
|
Sources
more coming soon








No comments:
Post a Comment