perpendicular lines:

In elementary geometry, the property of being perpendicular(perpendicularity) is the relationship between two lines which meet at a right angle (90 degrees). The property extends to other related geometric objects. A line is said to be perpendicular to another line if the two lines intersect at a right angle.

Perpendicular

It just means at right angles (90°) to.

The red line is perpendicular to the blue line in both these cases:

(The little box drawn in the corner, means "at right angles", so we didn't really need to also show that it was 90°, but we just wanted to!)

Parallel

Lines are parallel if they are always the same distance apart (called "equidistant"), and will never meet. (They also point in the same direction). Just remember:

Always the same distance apart and never touching.

example 2

The red line and blue line are parallel in both these examples:

Example 1

Perpendicular to Parallel

Question: What is the difference between perpendicular and parallel? 
Answer: 90 degrees (a right angle)
That's right, when we rotate a perpendicular line by 90° it becomes parallel (but not if it touches!)

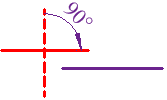Perpendicular ...	Rotate One Line 90°	... Parallel !

Likewise, parallel lines become perpendicular when one line is rotated 90°.

Parallel Curves

Curves can also be parallel when they are always the same distance apart (called "equidistant"), and never meet. Just like railroad tracks.
The red curve is parallel to the blue curve in both these cases:

Parallel Surfaces

Surfaces can also be parallel, so long as the rule still holds: always the same distance apart and never touching.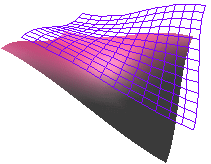

Lines and Planes

Advanced Topic: You can also learn about Parallel and Perpendicular Lines and Planes

 https://www.mathsisfun.com/perpendicular-parallel.html

Perpendicular Lines

Let's graph these lines:

* I'm using y = mx + b stuff to graph them!
 

These lines are perpendicular. (They form a angle.) So, what's going on with the slopes? Notice that they are inverses but the signs are different

A typical math book would say:

But this is easier:

You flip it over and change the sign -- That's how you get the slopes of perpendicular lines.

* If you want to be a super geek, you can rap it!

Check it out:

Take the 2 ... Write it as a fraction: 

Flip it over:   ... and change the sign: 

Let's do a problem:

Let's find the equation of the line that passes through the point
( 1 , 3 ) and is perpendicular to the line		.

What do we need?

a point

a slope

STEP 1:  Find the slope

It's perpendicular to

...

So, we'll get this guy's slope ...  flip it and change the sign!  Easy!

STEP 2: Use the point-slope formula with ( 1 , 3)              and m = 

Graph		and		and see if they
really look perpendicular.

---

TRY IT:

Find the equation of the line that passes through the point ( -2 , 2 ) and is perpendicular to the line

http://www.coolmath.com/algebra/08-lines/14-perpendicular-lines-03

Perpendicular lines (Coordinate Geometry) When two lines are perpendicular, the slope of one is the negative reciprocal of the other. If the slope of one line is m, the slope of the other is  Try this Drag points C or D. Note the slopes when the lines are at right angles to each other. When two lines are perpendicular to each other (at right angles or 90°), their slopes have a particular relationship to each other. If the slope of one line is m then the slope of the other line is the negative reciprocal of m, or So for example in the figure above, the line AB has a slope of 0.5, meaning it goes up by a half for every one across. The line CD if it is perpendicular to AB has a slope of -1/0.5 or -2. Adjust points C or D to make CD perpendicular to AB and verify this result. Fig 1. Lines are still perpendicular Remember that the equation works both ways, so it doesn't matter which line you start with. In the figure above the slope of CD is -2. So the slope of AB when perpendicular is Note too that the lines to do not have to intersect to be perpendicular. In Fig 1, the two lines are perpendicular to each other even though they do not touch. The slope relationship still holds. Example 1.   Are two lines perpendicular? Fig 1. Are these lines perpendicular? In Fig 1, the line AB and a line segment CD appear to be at right angles to each other. Determine if this is true. To do this, we find the slope of each line and then check to see if one slope is the negative reciprocal of the other. If the lines are perpendicular, each will be the negative reciprocal of the other. It doesn't matter which line we start with, so we will pick AB:  Calculator So, the slope of CD is -2.22, and the negative reciprocal of the slope of AB is -2.79. These are not the same, so the lines are not perpendicular, even though they look it. If you look carefully at the diagram, you can see that the point C is a little too far to the left for the lines to be perpendicular. Example 2. Define a line through a point perpendicular to a line In Fig 1, find a line through the point E that is perpendicular to CD. The point E is on the y-axis and so is the y-intercept of the desired line. Once we know the slope of the line, we can express it using its equation in slope-intercept form y=mx+b, where m is the slope and b is the y-intercept. First find the slope of the line CD: The line we seek will have a slope which is the negative reciprocal of this: The intercept is 10, the point where the line will cross the y-axis. Substituting these values into the equation, the line we need is described by the equation y = 0.45x + 10 This is one of the ways a line can be defined and so we have solved the problem. If we wanted to plot the line, we would find another point on the line using the equation and then draw the line through that point and the intercept. For more on this see Equation of a Line (slope - intercept form) http://www.mathopenref.com/coordperpendicular.html